D.8 Regresión no paramétrica
No se supone ninguna forma concreta en el efecto de las variables explicativas: \[Y=f\left( \mathbf{X}\right) +\varepsilon,\] con f función “cualquiera” (suave).
Métodos disponibles en
R:Regresión local (métodos de suavizado):
loess(),KernSmooth,sm, …Modelos aditivos generalizados (GAM):
gam,mgcv, ……
D.8.1 Modelos aditivos
Se supone que: \[Y=\beta_{0}+f_{1}\left( \mathbf{X}_{1}\right) +f_{2}\left( \mathbf{X}_{2}\right) +\cdots+f_{p}\left( \mathbf{X}_{p}\right) +\varepsilon\text{,}\] con \(f_{i},\) \(i=1,...,p,\) funciones cualesquiera.
Los modelos lineales son un caso particular considerando \(f_{i}(x) = \beta_{i}x\).
Son mucho más flexibles pero siguen siendo fáciles de interpretar.
Adicionalmente se puede considerar una función link: Modelos aditivos generalizados (GAM)
Hastie, T.J. y Tibshirani, R.J. (1990). Generalized Additive Models. Chapman & Hall.
Wood, S. N. (2006). Generalized Additive Models: An Introduction with R. Chapman & Hall/CRC
Utilizaremos como ejemplo el conjunto de datos Prestige de la librería carData
(Companion to Applied Regression Data Sets, paquete car).
Se tratará de explicar prestige (puntuación de ocupaciones obtenidas a traves
de una encuesta) a partir de income (media de ingresos en la ocupación) y
education (media de los años de educación).
library(mgcv)
data(Prestige, package = "carData")
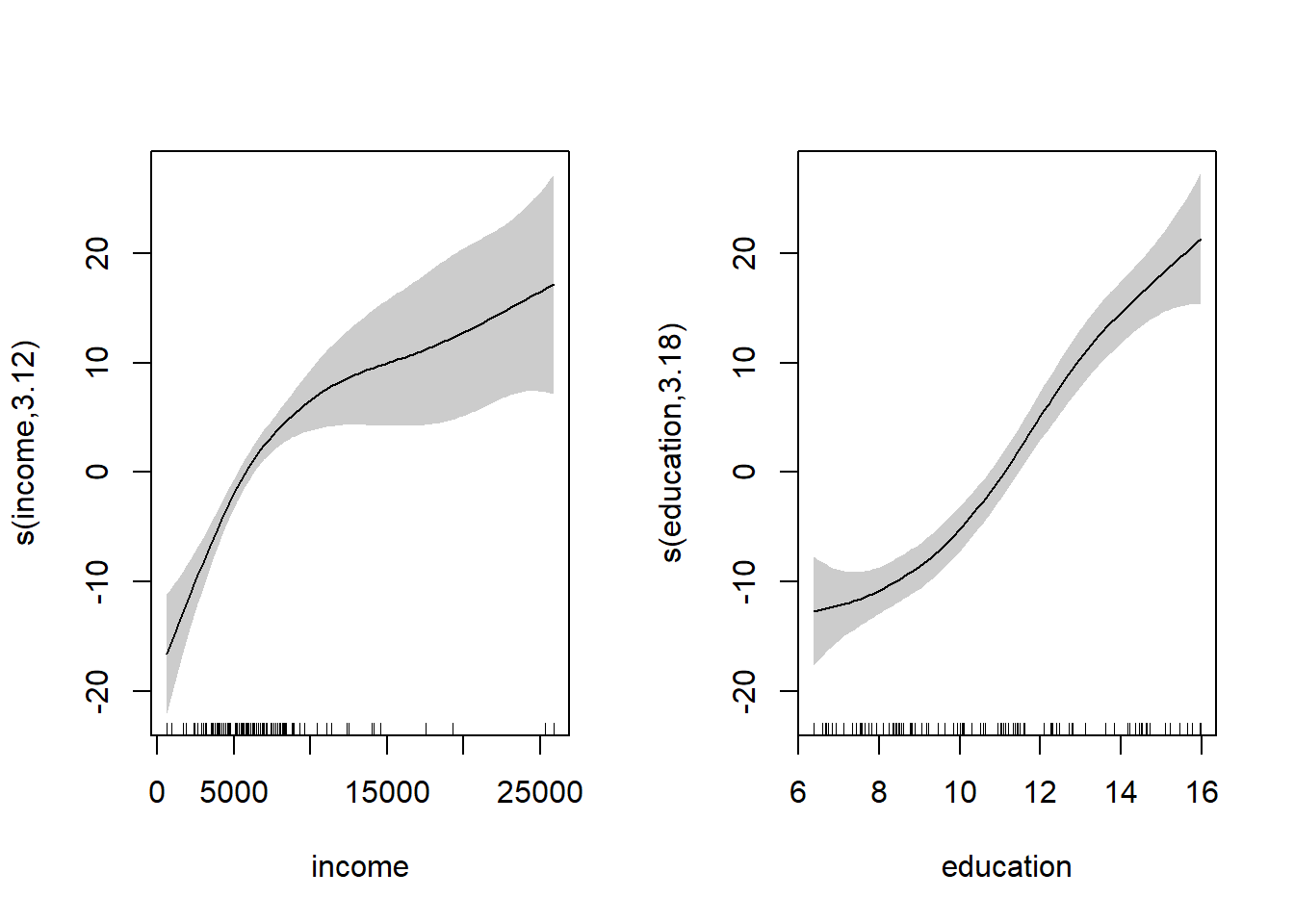
modelo <- gam(prestige ~ s(income) + s(education), data = Prestige)
summary(modelo)##
## Family: gaussian
## Link function: identity
##
## Formula:
## prestige ~ s(income) + s(education)
##
## Parametric coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 46.8333 0.6889 67.98 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Approximate significance of smooth terms:
## edf Ref.df F p-value
## s(income) 3.118 3.877 14.61 1.53e-09 ***
## s(education) 3.177 3.952 38.78 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## R-sq.(adj) = 0.836 Deviance explained = 84.7%
## GCV = 52.143 Scale est. = 48.414 n = 102En este caso la función plot representa los efectos (parciales) estimados de
cada covariable: