D.7 Métodos de regularización

Estos métodos emplean también un modelo lineal generalizado, pero imponen restricciones adicionales a los parámetros que los “retraen” (shrink) hacia cero:

• Produce una reducción en la varianza de predicción (a costa del sesgo).

• En principio se consideran todas las variables explicativas.

Por ejemplo, en el caso del modelo lineal: \[Y=\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\cdots+\beta_{p}X_{p}+\varepsilon\]

En lugar de ajustarlo por mínimos cuadrados (estándar), minimizando: \[ RSS = \sum\limits_{i=1}^{n}\left( y_{i} - \beta_0 - \beta_1 x_{1i} - \cdots - \beta_p x_{pi} \right)^{2}\]

Ridge regression

• Penalización cuadrática: \(RSS+\lambda\sum_{j=1}^{p}\beta_{j}^{2}\).

Lasso

• Penalización en valor absoluto: \(RSS+\lambda\sum_{j=1}^{p}|\beta_{j}|\).

• Normalmente asigna peso nulo a algunas variables (selección de variables).

El parámetro de penalización se selecciona por validación cruzada.

• Normalmente estandarizan las variables explicativas (coeficientes en la misma escala).

Consideraremos como ejemplo el conjunto de datos hatco.RData que contiene observaciones de clientes de la compañía de distribución industrial (Compañía Hair, Anderson y Tatham).

load('data/hatco.RData')
as.data.frame(attr(hatco, "variable.labels"))

##          attr(hatco, "variable.labels")
## empresa                         Empresa
## tamano             Tamaño de la empresa
## adquisic      Estructura de adquisición
## tindustr              Tipo de industria
## tsitcomp    Tipo de situación de compra
## velocida           Velocidad de entrega
## precio                 Nivel de precios
## flexprec        Flexibilidad de precios
## imgfabri          Imagen del fabricante
## servconj              Servicio conjunto
## imgfvent     Imagen de fuerza de ventas
## calidadp            Calidad de producto
## fidelida   Porcentaje de compra a HATCO
## satisfac            Satisfacción global
## nfidelid        Nivel de compra a HATCO
## nsatisfa          Nivel de satisfacción

Consideraremos como respuesta la variable fidelida y como variables explicativas el resto de variables continuas menos satisfac.

library(glmnet)

El paquete glmnet no emplea formulación de modelos, hay que establecer la respuesta y y las variables explicativas x (se puede emplear la función model.matrix() para construir x, la matriz de diseño, a partir de una fórmula). En este caso, eliminamos también la última fila por tener datos faltantes:

x <- as.matrix(hatco[-100, 6:12])
y <- hatco$fidelida[-100]

D.7.1 Ridge Regression

Ajustamos un modelo de regresión ridge con la función glmnet con alpha=0 (ridge penalty).

fit.ridge <- glmnet(x, y, alpha = 0)
plot(fit.ridge, xvar = "lambda", label = TRUE)

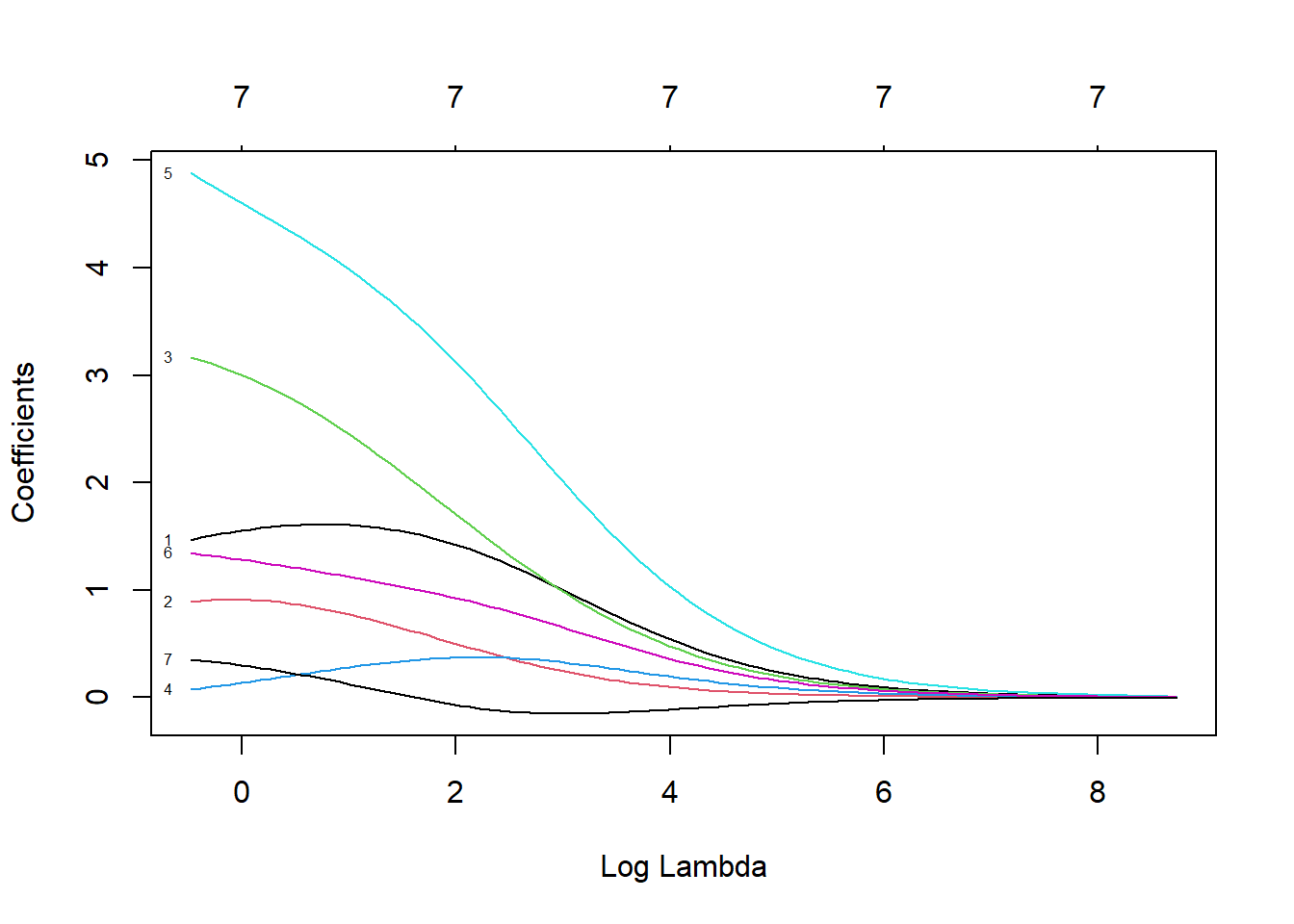
Para seleccionar el parámetro de penalización por validación cruzada se puede emplear la función cv.glmnet.

cv.ridge <- cv.glmnet(x, y, alpha = 0)
plot(cv.ridge)

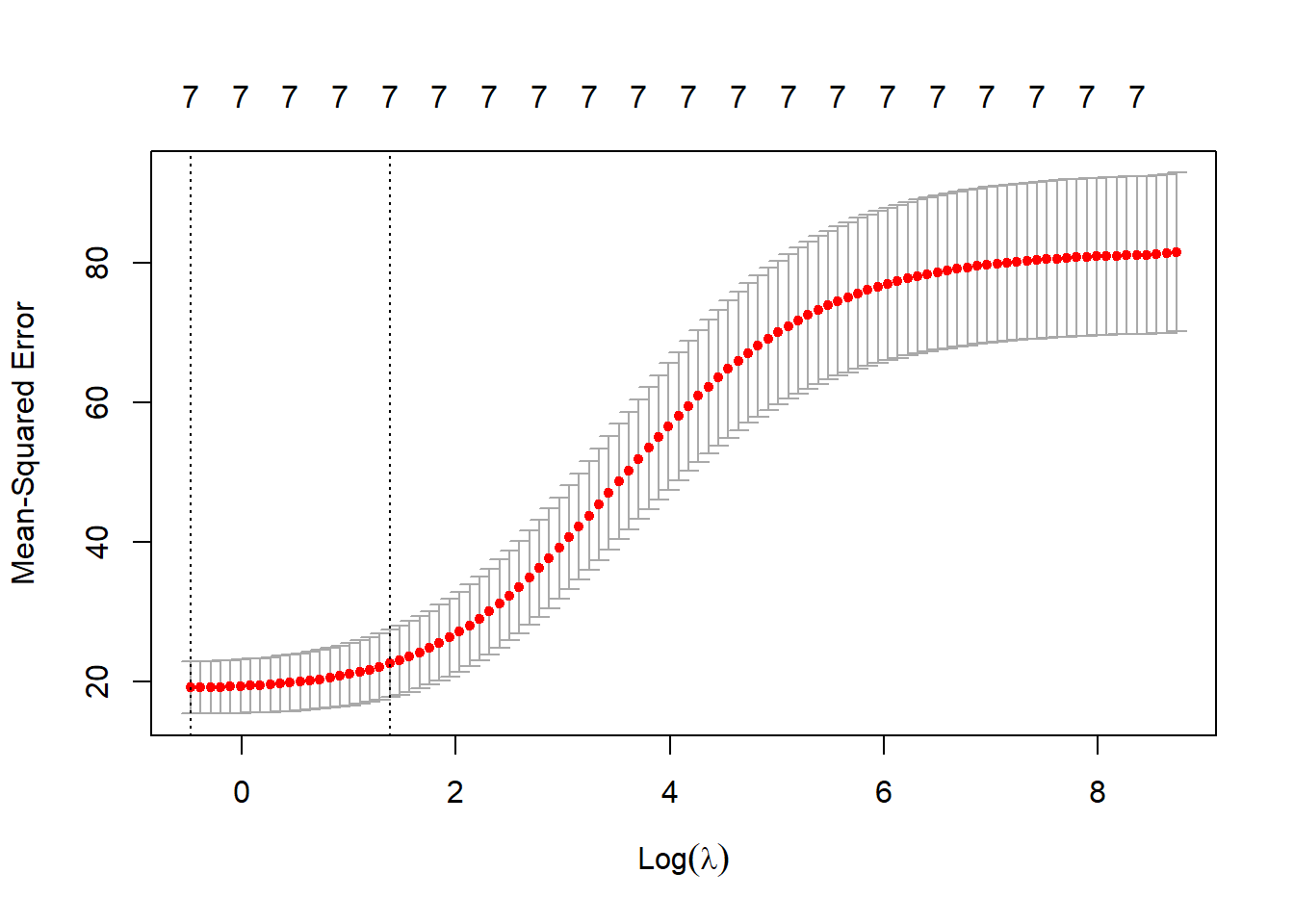
En este caso el parámetro sería:

cv.ridge$lambda.1se

## [1] 3.989587

y el modelo resultante contiene todas las variables explicativas:

coef(cv.ridge)

## 8 x 1 sparse Matrix of class "dgCMatrix"
##                      1
## (Intercept) 6.25898621
## velocida    1.56785760
## precio      0.67897678
## flexprec    2.17894174
## imgfabri    0.32939271
## servconj    3.69427361
## imgfvent    1.05562044
## calidadp    0.04709431

D.7.2 Lasso

Ajustamos un modelo lasso también con la función glmnet (con la opción por defecto alpha=1, lasso penalty).

fit.lasso <- glmnet(x,y)
plot(fit.lasso, xvar = "lambda", label = TRUE)

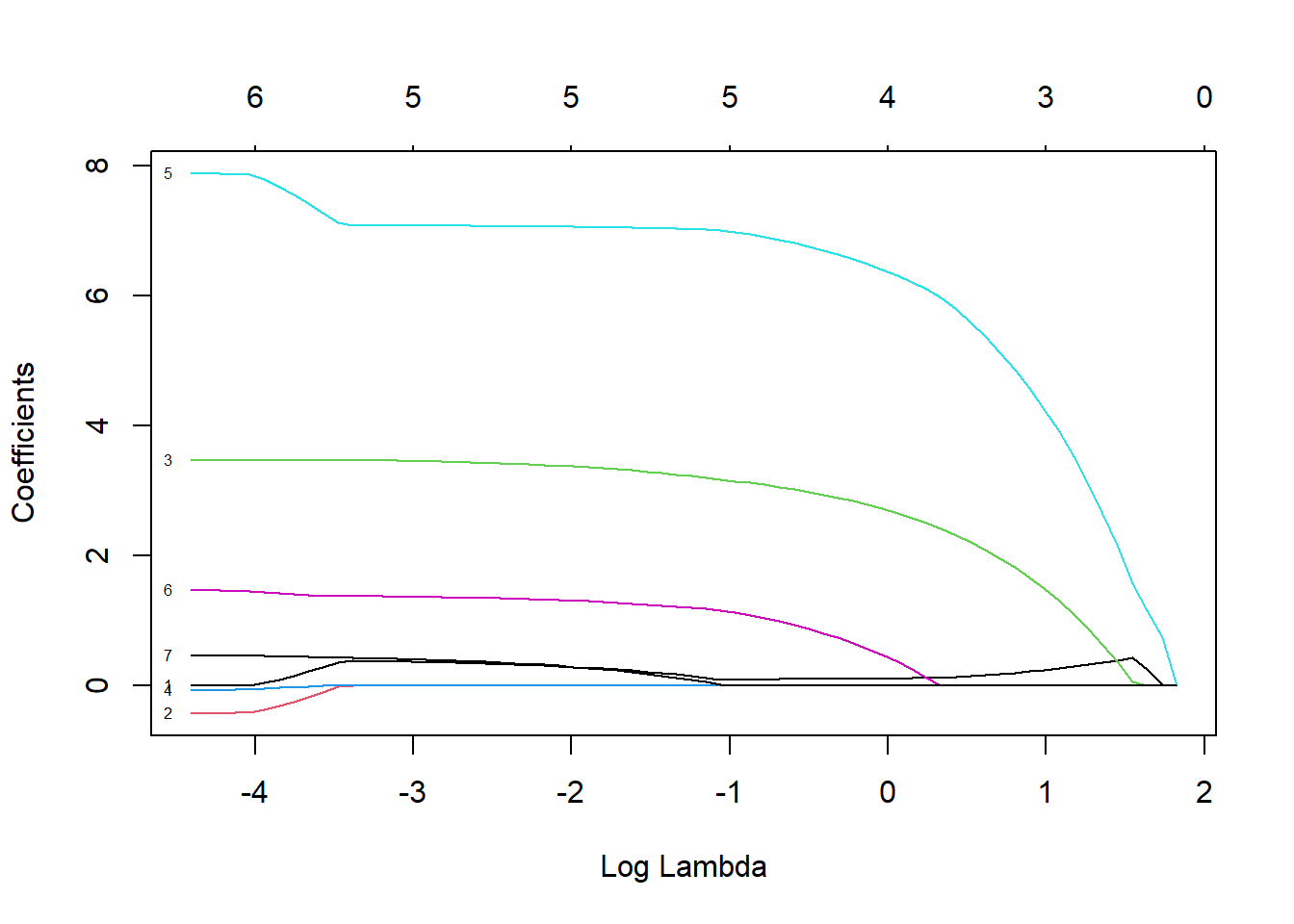
Seleccionamos el parámetro de penalización por validación cruzada.

cv.lasso <- cv.glmnet(x,y)
plot(cv.lasso)

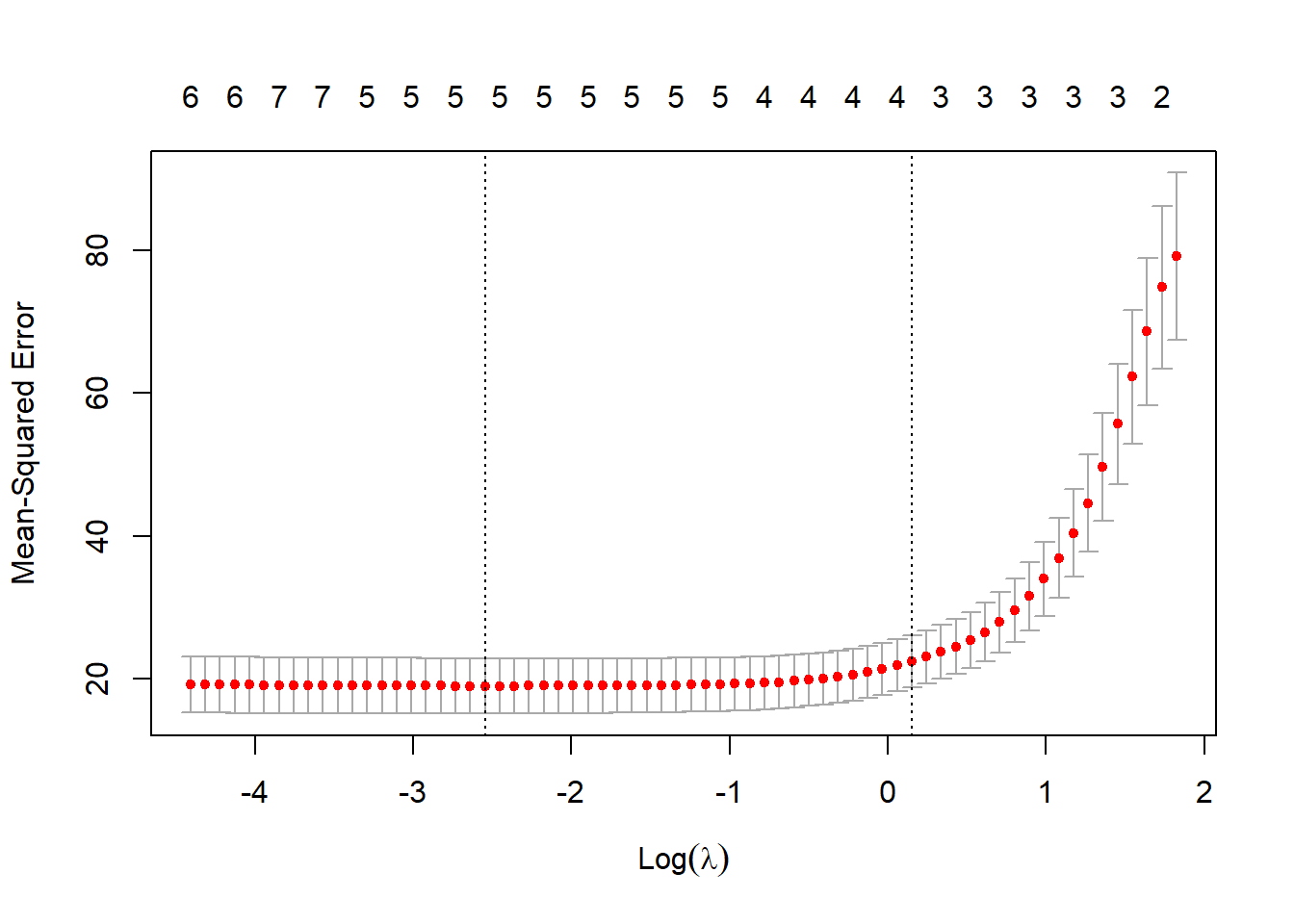
En este caso el modelo resultante solo contiene 4 variables explicativas:

coef(cv.lasso)

## 8 x 1 sparse Matrix of class "dgCMatrix"
##                     1
## (Intercept) 6.7318222
## velocida    0.1070413
## precio      .        
## flexprec    2.5781037
## imgfabri    .        
## servconj    6.2106583
## imgfvent    0.2446890
## calidadp    .